昨天說到,如果二元搜尋樹是 skewed tree 的話,那麼 insert / delete / search 有可能就會因此變成 O(n) 時間。
因此,若能將高度平衡,即可以讓其時間在 O(logn) 等級。
其實 AVL Tree 不是甚麼樹縮寫,而是發明者的縮寫(Adelson-Velsky and Landis)
是一棵二元搜尋樹(Binary Search Tree),可為空樹,若非空,則:
每個節點的平衡係數,等於 HL - HR。
根據定義,AVL Tree 所有節點的平衡係數只能是三種數值:-1、0、1
圖示:
(來源:https://en.wikipedia.org/wiki/AVL_tree)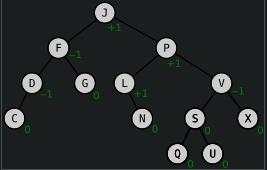

-768.png)
-768.png)
-768.png)
AVL Tree 的建立就是靠不斷的插入節點,在進行 rotation。
例如:2 5 8 4 3 1 依序插入,建立 AVL Tree
解:(紅字為 BF)
這裡只是簡單介紹定義,不會介紹他的操作,因為太麻煩了。
二元樹允許很多形式,但當樹呈現斜曲時,可能會讓操作時間變久。透過 rotation 將 BST 轉換為 RB tree 或 AVL Tree,可以讓樹保持平衡,時間在 O(logn)等級。
明天則是來介紹另一種二元樹的結構: Heap
